Kalman Filter

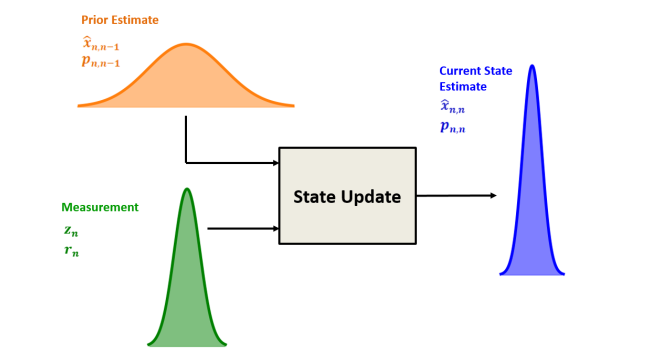
Deriving the Kalman Gain

State Estimate:

$${\hat{x}}_{n,n}=w_1{z}_n+w_2{\hat{x}}_{n,n-1}$$

Where:

• $w_1$ is the weight of the measurement
• $w_2$ is the weight of the prior state estimate

If $w_1=1$ means that we are 100% certain that the measurement is trustworthy. Therefore, $1-w_2=w_1$, which means that the probability of $w_1$ is the probability of $w_2$ not happening.

Therefore,

$${\hat{x}}_{n,n}=w_1{z}_n+(1-w_1){\hat{x}}_{n,n-1}$$

Accounting for relation between variances,

$$p_{n,n}=w_1^2{r}_n+(1-w_1{)}^2{p}_{n,n-1}$$

Where:

• $p_{n,n}$ is variance of the optimum combined estimate
• $p_{n,n-1}$ is the variance of the prior estimate ${\hat{x}}_{n,n-1}$
• $r_n$ is the variance of the measurement $z_n$

Note

Recall that for any normally distributed random variable $x$ with variance ${\sigma }^2$, $kx$ is distributed normally with variance $k^2{\sigma }^2$.

We have to minimize $p_{n,n}$ in order to get the optimum estimate, therefore, we have to find $w_1$ such that it minimizes $p_{n,n}$.

This is achievable by differentiating $p_{n,n}$ with respect to $w_1$ and setting the result equal to zero.

$\frac{d{p}_{n,n}}{d{w}_1}=2w_1{r}_n-2(1-w_1)p_{n,n-1}$

$$2w_1{r}_n-2(1-w_1)p_{n,n}=0$$

Solving,

$$w_1{r}_n=p_{n,n-1}-w_1{p}_{n,n-1}$$ $$w_1{r}_n+w_1{p}_{n,n-1}=p_{n,n-1}$$ $$w_1=\frac{p_{n,n-1}}{r_n+p_{n,n-1}}$$

Substituting the result back into the current state estimation,

$${\hat{x}}_{n,n}=w_1{z}_n+(1-w_1){\hat{x}}_{n,n-1}$$ $${\hat{x}}_{n,n}=w_1{z}_n-w_1{\hat{x}}_{n,n-1}+{\hat{x}}_{n,n-1}$$ $${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+w_1(z_n-{\hat{x}}_{n,n-1})$$ $${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\frac{p_{n,n-1}}{r_n+p_{n,n-1}}(z_n+{\hat{x}}_{n,n-1})$$

Here we can see that $w_1$ is the Kalman Gain $K_t$.

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+K_t(z_n+{\hat{x}}_{n,n-1})$$